Из O(n) в O(1): Сила Префиксных Сумм

BACK TO BLOG

Из O(n) в O(1): Сила Префиксных Сумм

Префиксные Суммы (Prefix Sum) является простой, но мощной техникой, которая учит эффективности: не пересчитывать заново, а использовать уже накопленные результаты.
Благодаря нему за один проход по массиву можно найти ответы на любые диапазонные запросы за O(1).
Эта идея лежит в основе десятков задач LeetCode и формирует настоящую алгоритмическую

Что такое `Prefix Sum`?

Это алгоритмическая техника накопления промежуточных результатов при обходе массива.

Префиксные суммы: на позиции i хранится сумма (или другой агрегат) элементов от начала до i.
Суффиксные суммы: на позиции i хранится сумма от i до конца массива.

Главная идея: хранить частичные результаты, чтобы отвечать на запросы «сумма на отрезке» или «остаток после позиции» за O(1), а не пересчитывать каждый раз.

Зачем это нужно?

Быстро отвечать на запросы «сумма диапазона» (например, с 2-го по 5-й заказ).
Используется как строительный блок во многих алгоритмах: динамическое программирование, скользящее окно, подмассивы с ограничениями.

Где применяются в реальной жизни?

Техника префиксных сумм не только про алгоритмы и LeetCode.
Она встречается в самых разных системах, где нужно быстро получать агрегированные данные без повторных вычислений.

Бизнес-аналитика: расчёт выручки, количества заказов и активности пользователей за периоды без пересчёта.
Финансы: вычисление расходов и остатков по датам (разница между накопленными балансами).
Игры: подсчёт очков и опыта за промежутки времени.
Аналитика данных / ML: ускорение вычислений скользящих средних и агрегатов по временным рядам.
Мониторинг: мгновенные ответы на запросы вроде «сколько запросов за последние 5 минут».

👉 Везде, где нужно быстро узнать «сколько накопилось между двумя точками», префиксные суммы дают ответ за O(1).

Как это работает?

Вместо пересчёта суммы каждый раз, один проход сохраняет промежуточные результаты.

Псевдокод для префиксных сумм:

prefix[0] = array[0]                        // база: первый элемент
для i от 1 до n-1:
    prefix[i] = prefix[i-1] + array[i]      // накапливаем сумму до текущего индекса

👉 Теперь сумма на подотрезке [l, r] вычисляется за O(1):

range_sum = prefix[r] - prefix[l-1]

Псевдокод для суффиксных сумм:

suffix[n-1] = array[n-1]                    // база: последний элемент
для i от n-2 до 0:
    suffix[i] = suffix[i+1] + array[i]      // накапливаем сумму справа налево

Аналогия из жизни: денежные накопления

Представьте, что вы каждую неделю откладываете деньги на депозит.
Банк показывает вам только общий накопленный баланс за каждую неделю:

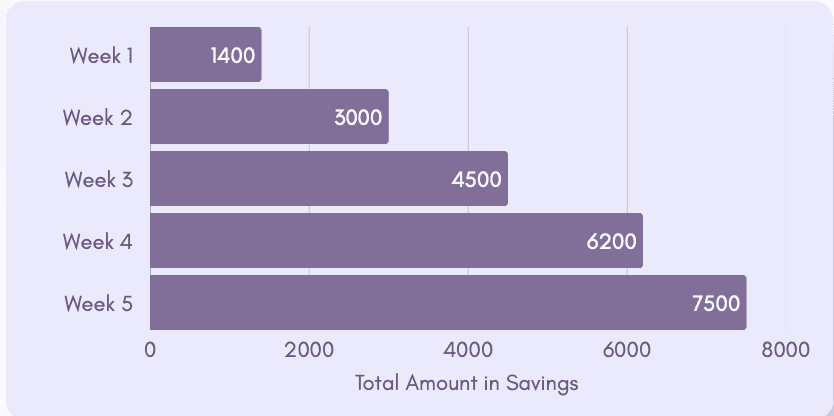
📅 Неделя 1 → 1400 ₸
📅 Неделя 2 → 3000 ₸
📅 Неделя 5 → 7500 ₸

Теперь вам нужно узнать: а сколько вы отложили только на 4-й и 5-й неделях?

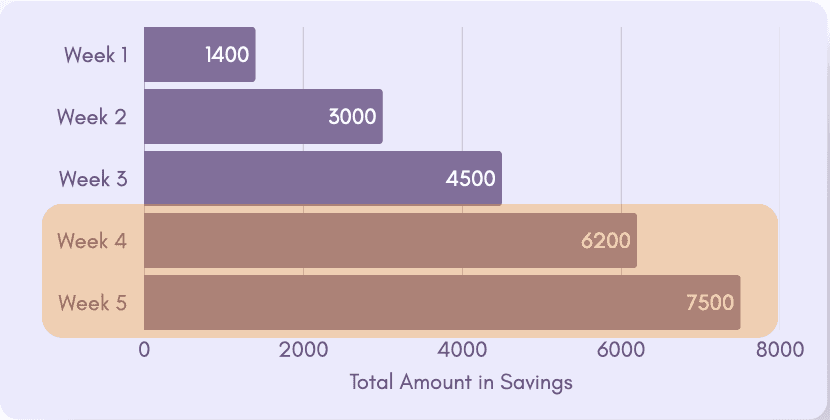
Мы знаем:

К 5-й неделе у вас накоплено 7500 ₸.
К 3-й неделе было 4500 ₸ (предположим для примера).

Тогда:
👉 Сумма, отложенная на неделях 4 и 5 = 7500 – 4500 = 3000 ₸

Почему отнимаем баланс на 3-й неделе?
Потому что хотим "обнулить" всё, что было накоплено раньше до 4-й недели. Это как будто вы начали копить с чистого листа с 4-й недели.

Именно это и делает формула префиксной суммы в программировании:
range_sum(i, j) = prefix[j] – prefix[i – 1]

prefix[j]: это сумма до конца интервала
prefix[i – 1]: это всё, что было до начала интервала
Их разность является суммой в нужном диапазоне

Визуализация

Исходный массив:

orders = [2, 3, 5, 4]

Префиксные суммы:

prefix = [2, 5, 10, 14]

(каждый элемент = сумма от начала до текущего, слева направо)

Суффиксные суммы:

suffix = [14, 12, 9, 4]

(каждый элемент = сумма от текущего до конца, справа налево)

Практические задачи

1. Сумма продаж за диапазон

/*
 * Problem: Range Sales Sum
 *
 * Дан массив дневных продаж (в тенге).
 * Нужно найти сумму продаж между индексами l и r включительно.
 * Использовать префиксные суммы для ускорения вычисления.
 *
 * Пример:
 * Ввод: sales = [10, 20, 30, 40, 50], l = 1, r = 3
 * Вывод: 90  // (20 + 30 + 40)
 *
 * Constraints:
 * - Длина массива ≤ 10^5.
 * - 0 ≤ l ≤ r < sales.length
 *
 * Note:
 * Тренирует построение массива prefix[] и вычисление суммы на диапазоне.
 * Подготавливает к задачам вроде LeetCode 1480 (Running Sum).
 */
public int rangeSalesSum(int[] sales, int l, int r) {
}

Остаток кофе (суффиксные суммы)

/*
 * Problem: Remaining Coffee
 *
 * Бариста имеет список заказов в граммах кофе.
 * В мешке всего N грамм. После каждого заказа нужно определить,
 * сколько кофе осталось.
 *
 * Пример:
 * Ввод: orders = [5, 7, 3, 2], total = 20
 * Вывод: [15, 8, 5, 3]
 * Объяснение:
 * - После первого заказа: 20 - 5 = 15
 * - После второго: 15 - 7 = 8
 * - После третьего: 8 - 3 = 5
 * - После четвёртого: 5 - 2 = 3
 *
 * Constraints:
 * - Длина массива ≤ 10^5.
 * - Все значения положительные.
 *
 * Note:
 * Тренирует вычисление суффиксных сумм — движение справа налево.
 * Демонстрирует идею "остатка" вместо "накопления".
 */
public int[] remainingCoffee(int[] orders, int total) {
}

Типичные ошибки

Неправильная база
Если начать с prefix[0] = 0, то формулы для диапазона и индексов будут сдвинуты. Нужно чётко определить базовый случай.
Off-by-one в диапазонах
Легко ошибиться: [l, r] считается как prefix[r] - prefix[l-1]. Если забыть -1, результат будет неверным.
Путают префикс и суффикс
Нужно помнить: префикс идёт слева направо, суффикс — справа налево.

Результат

Техника префиксных и суффиксных сумм учит мыслить через накопление: не пересчитывать заново, а сохранять промежуточные итоги. Это фундамент для оптимизации многих алгоритмов.